
Daftar Isi :
Sifat-Sifat Determinan Matriks
Kenapa sih kita harus belajar sifat-sifat determinan?

Untuk mengetahui alasannya, mari kita umpamakan nilai determinan yang kita cari ibarat sebuah layang-layang yang nyangkut di pucuk pohon yang penuh dengan cabang dan sifat-sifat determinan sebagai tangga.
Nah, dari sini ada dua opsi utama untuk mendapatkan layang-layang tersebut, yaitu pertama dengan memanjat pohonnya langsung (menghitung determinan dengan cara umum seperti ekspansi kofaktor atau lainnya) dan opsi kedua menggunakan tangga untuk naik ke atas pohon tersebut.
Kedua pilihan tersebut sama-sama dapat mengambil layangan, namun akan lebih efisien dan efektif jika kita menggunakan bantuan tangga untuk naik pohon dan mendapatkan layangan tersebut.
Dari perumpamaan di atas, kita dapat mempermudah perhitungan dalam mencari determinan dengan memanfaatkan sifat-sifat determinan sebagai berikut :
Sifat 1
Jika matriks \(A\) dan \(B\) adalah matriks persegi yang berordo sama maka
Contoh 1
MIsalkan \(A, B\) dan \(C\) adalah matriks persegi yang mempunyai ordo yang sama, dengan \(C=AB\).
Tentukan determinan dari matriks \(C\).
Penyelesaian :
Cara pertama, kita lakukan operasi perkalian matriks, sehingga didapat :
$$\begin{aligned}C&=AB\\&=\left[{\begin{array}{cc}-3&1\\0&2\end{array}}\right]\left[{\begin{array}{cc}2&-3\\-4&5\end{array}}\right]\\&=\left[{\begin{array}{cc}-6-4&9+5\\0-8&0+10\end{array}}\right]\\&=\left[{\begin{array}{cc}-10&14\\-8&10\end{array}}\right]\end{aligned}$$
Kemudian kita hitung determinan dari matriks \(C\)
$$\begin{aligned}\text{det}(C)&=\left|{\begin{array}{cc}-10&14\\-8&10\end{array}}\right|\\&=-100-(-112)\\&=12\end{aligned}$$
Cara kedua, kita gunakan sifat 1, sehingga
Setelah kita amati ternyata dua cara di atas mempunyai hasil akhir yang sama, namun dari segi efisiensi lebih baik cara kedua.
Sifat 2
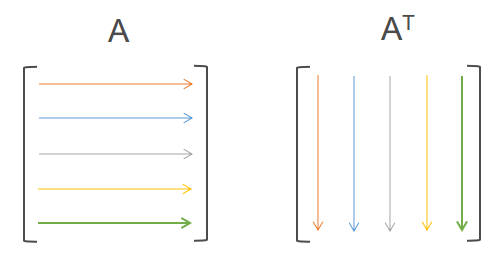
Jika \(A\) adalah matriks persegi dan \(A^{T}\) adalah transpose matriks \(A\), maka berlaku
$$\boxed{\text{det}(A)=\text{det}\left({A^{T}}\right)}$$
Contoh 2
Misalkan matriks \(A\) didefinisikan sebagai berikut :
$$A=\left[{\begin{array}{cc}1&2\\3&4\end{array}}\right]$$
Tentukanlah nilai dari \(\text{det}\left({A^{T}}\right)\)
Penyelesaian :
Cara pertama (manual) dengan mentranspose matriks \(A\)
$$A^{T}=\left[{\begin{array}{cc}1&3\\2&4\end{array}}\right]$$
Selanjutnya menghitung determinan dari \(A^{T}\)
$$\begin{aligned}\text{det}\left({A^{T}}\right)&=\left|{\begin{array}{cc}1&3\\2&4\end{array}}\right|\\&=4-6\\&=-2\end{aligned}$$
Cara kedua menggunakan sifat
$$\begin{aligned}\text{det}\left({A^{T}}\right)&=\text{det}(A)\\&=\left|{\begin{array}{cc}1&2\\3&4\end{array}}\right|\\&=4-6\\&=-2\end{aligned}$$
Sifat 3
Jika A adalah matriks diagonal atau matriks skalar, maka
$$\boxed{\text{det}(A)=a_{11}\times a_{22}\times\dots\times a_{nn}}$$
(Determinan \(A\) adalah perkalian semua entri pada diagonal utama)
Contoh 3
Diberikan matriks \(A\) sebagai berikut :
$$A=\left[{\begin{array}{ccc}\sqrt{2}&0&0\\0&-2&0\\0&0&\frac{1}{2}\end{array}}\right]$$
Tentukan determinan matriks \(A\)
Penyelesaian :
Cara pertama menggunakan aturan sarrus, atau dapat dituliskan :
$$\left[{\begin{array}{ccc|cc}\sqrt{2}&0&0&\sqrt{2}&0\\0&-2&0&0&-2\\0&0&\frac{1}{2}&0&0\end{array}}\right]$$
sehingga determinan dari \(A\) yakni :
Cara kedua dengan menggunakan sifat didapat :
$$\begin{aligned}\text{det}(A)&=\left|{\begin{array}{ccc}\sqrt{2}&0&0\\0&-2&0\\0&0&\frac{1}{2}\end{array}}\right|\\&=\sqrt{2}\times-2\times\frac{1}{2}\\&=-\sqrt{2}\end{aligned}$$
Sifat 4
Jika \(A\) adalah matriks segitiga (atas/bawah) maka
$$\boxed{\text{det}(A)=a_{11}\times a_{22}\times\dots\times a_{nn}}$$
(Determinan \(A\) adalah perkalian semua entri pada diagonal utama)
Contoh 4
Misalkan diberikan matriks \(A_{3\times3}=[a_{ij}]\) sebagai berikut :
$$A=\left[{\begin{array}{ccc}\pi&\frac{3}{4}&-1\\0&2&2\sqrt{3}\\0&0&\frac{3}{2}\end{array}}\right]$$
Tentukan determinan dari matriks \(A\)
Penyelesaian :
Cara pertama : Jika pada contoh 3, kita telah menggunakan metode sarrus. Sekarang kita akan menggunakan metode ekspansi kofaktor pada kolom pertama \((a_{11}=\pi,a_{21}=0,a_{31}=0)\).
Cara kedua menggunakan sifat maka :
$$\begin{aligned}\text{det}(A)&=a_{11}\times a_{22}\times a_{33}\\&=\pi\times2\times\frac{3}{2}\\&=3\pi\end{aligned}$$
Sifat 5
Jika \(A\) adalah matriks persegi berordo \(n\times n\) dan \(k\) adalah sebarang bilangan maka
$$\boxed{\text{det}(kA)=k^{n}\times \text{det}(A)}$$
Contoh 5
Diketahui :
$$A=\left[{\begin{array}{cc}2&4\\6&8\end{array}}\right]$$
Tentukan determinan dari \(3A\)
Penyelesaian :
Cara pertama, dengan mengalikan matriks \(A\) dengan 3 sehingga didapat :
$$\begin{aligned}3A&=3\times \left[{\begin{array}{cc}2&4\\6&8\end{array}}\right]\\&=\left[{\begin{array}{cc}6&12\\18&24\end{array}}\right]\end{aligned}$$
Kemudian kita hitung determinannya.
$$\begin{aligned}\text{det}(3A)&=\left|{\begin{array}{cc}6&12\\18&24\end{array}}\right|\\&=(6)(24)-(12)(18)\\&=-72\end{aligned}$$
Cara kedua dengan menggunakan sifat.
$$\begin{aligned}\text{det}(3A)&=3^{2}\times\text{det}(A)\\&=9\times \left|{\begin{array}{cc}2&4\\6&8\end{array}}\right|\\&=9(16-24)\\&=-72\end{aligned}$$
Sifat 6
Jika matriks \(A\) dapat dibalik (invertible) atau mempunyai invers, maka
$$\boxed{\text{det}\left({A^{-1}}\right)=\frac{1}{\text{det}(A)}}$$
Contoh 6
Diketahui :
$$A=\left[{\begin{array}{cc}-4&1\\2&3\end{array}}\right]$$
Tentukan nilai determinan dari \(A^{-1}\)
Penyelesaian :
Cara pertama :
Umumnya pada saat kita mencari invers dari matriks \(A_{2\times2}=[a_{ij}]\), kita menggunakan rumus :
$$A^{-1}=\frac{1}{\text{det}(A)}\left[{\begin{array}{cc}a_{22}&-a_{12}\\-a_{21}&a_{11}\end{array}}\right]$$
Sehingga berdasarkan rumus di atas kita dapatkan :
$$\begin{aligned}A^{-1}&=\frac{1}{-12-2}\left[{\begin{array}{cc}3&-1\\-2&-4\end{array}}\right]\\&=\left[{\begin{array}{cc}-\frac{3}{14}&\frac{1}{14}\\\frac{2}{14}&\frac{4}{14}\end{array}}\right]\end{aligned}$$
Selanjutnya kita hitung determinan dari \(A^{-1}\).
Cara kedua menggunakan sifat, kita peroleh :
$$\begin{aligned}\text{det}\left({A^{-1}}\right)&=\frac{1}{\text{det}\left({A}\right)}\\&=\frac{1}{-12-2}\\&=-\frac{1}{14}\end{aligned}$$
Baca juga : Cara mencari invers matriks dengan OBE
Sifat 7
Jika \(A\) adalah matriks persegi yang memuat baris nol atau kolom nol maka
$$\boxed{\text{det}(A)=0}$$
Contoh 7
Misalkan matriks \(A\) dan \(B\) didefinisikan sebagai berikut :
$$A=\left[{\begin{array}{ccc}1&0&2\\3&0&4\\5&0&6\end{array}}\right]$$
$$B=\left[{\begin{array}{ccc}5&4&3\\2&1&0\\0&0&0\end{array}}\right]$$
Tentukan nilai determinan \(A\) dan \(B\)
Pembuktian :
Cara pertama : dengan menggunakan metode ekspansi kofaktor, kita dapatkan :
(Ekspansi kofaktor sepanjang kolom kedua dari \(A\))
(Ekspansi kofaktor sepanjang baris ketiga dari \(B\))
Cara kedua dengan memanfaatkan sifat determinan, maka kita cukup mencermati baris-baris dan kolom-kolom pada matriks \(A\) dan \(B\), karena pada matriks \(A\) terdapat satu kolom (kolom kedua) yang semua entri-entrinya bernilai nol sehingga berdasarkan sifat ke-7 maka \(\text{det}(A)=0\) begitu pula pada matriks \(B\) karena terdapat satu baris (baris ketiga) yang entri-entrinya bernilai nol maka \(\text{det}(B)=0\).
Sifat 8
Jika \(A\) adalah matriks persegi dengan memuat dua baris yang saling berkelipatan atau dua kolom yang saling berkelipatan, maka
$$\boxed{\text{det}(A)=0}$$
Contoh 8
Tentukan determinan dari matriks berikut :
$$A=\left[{\begin{array}{ccc}-1&2&1\\3&-2&5\\-3&6&3\end{array}}\right]$$
Penyelesaian :
Berdasarkan aturan sarrus maka :
$$\left[{\begin{array}{ccc|cc}-1&2&1&-1&2\\3&-2&5&3&-2\\-3&6&3&-3&6\end{array}}\right]$$
Sehingga diperoleh :
Cara Alternatif yakni dengan memperhatikan baris-baris dan kolom-kolomnya, apabila terdapat dua baris atau dua kolomnya berkelipatan contohnya pada matriks \(A\), dimana baris ketiga merupakan kelipatan dari baris pertama. Sehingga berdasarkan sifat ke-8 ini maka \(\text{det}(A)=0\).
Sifat 9
Misalkan \(A_{1},A_{2},\dots A_{n}\) dan \(B\) adalah matriks persegi yang berordo sama yang hanya berbeda dalam satu baris tunggal, anggaplah perbedaan terletak pada baris ke-\(k\) kemudian kita misalkan lagi bahwa baris ke-\(k\) dari \(B\) diperoleh dengan menambahkan entri-entri yang bersesuaian dalam setiap baris ke-\(k\) dari \(A_{i}\) dengan \(i=\{1,2,3,\dots,n\}\), sehingga berlaku :
$$\boxed{\text{det}(B)=\sum_{i=1}^{n}\text{det}(A_{i})}$$
Persamaan di atas juga berlaku jika \(A_{1},A_{2},\dots A_{n}\) dan \(B\) hanya berbeda dalam satu kolom tunggal, dengan kolom yang berbeda (misalkan ke-\(j\)) dari B diperoleh dengan menambahkan entri-entri yang bersesuaian dari setiap kolom ke-\(j\) dari matriks \(A_{i}\).
Contoh 9
Misalkan matriks \(A, B\) dan \(C\) didefinisikan sebagai berikut :
Kita akan mencoba memperlihatkan bahwa berdasarkan sifat ke-9 ini maka \(\text{det}(C)=\text{det}(A)+\text{det}(B)\).
Pertama kita hitung nilai determinan dari matriks \(A, B\) dan \(C\).
$$\text{det}(A)=\left|{\begin{array}{ccc}1&2&-1\\\color{red}{5}&\color{red}{2}&\color{red}{0}\\1&2&3\end{array}}\right|=-32$$
$$\text{det}(B)=\left|{\begin{array}{ccc}1&2&-1\\\color{red}{-4}&\color{red}{3}&\color{red}{1}\\1&2&3\end{array}}\right|=44$$
$$\text{det}(C)=\left|{\begin{array}{ccc}1&2&-1\\\color{red}{1}&\color{red}{5}&\color{red}{1}\\1&2&3\end{array}}\right|=12$$
Untuk cara perhitungannya bisa menggunakan aturan sarrus atau ekspansi kofaktor dan proses perhitungannya sengaja tidak ditampilkan, untuk latihan bersama.
Sifat 10
Misalkan \(A\) adalah matriks persegi, kemudian \(A\) kita kenakan Operasi Baris Elementer maka berlaku :
- Jika \(A^{*}\) diperoleh dari \(A\) dengan cara mengalikan satu baris dari \(A\) dengan sembarang bilangan \(k\neq0\), maka \(\boxed{\text{det}\left({A^{*}}\right)=k\times \text{det}(A)}\)
- Jika \(A^{*}\) diperoleh dari \(A\) dengan cara menukar dua baris, maka \(\boxed{\text{det}\left({A^{*}}\right)=-\text{det}(A)}\)
- Jika \(A^{*}\) diperoleh dari \(A\) dengan cara menjumlahkan satu baris dengan kelipatan baris lain, maka \(\boxed{\text{det}\left({A^{*}}\right)=\text{det}(A)}\)
Untuk contohnya akan kita akan bahas bersama pada bagian selanjutnya. Pada bagian selanjutnya kita akan mengenal metode yang tak kalah unik dalam mencari nilai determinan yaitu metode reduksi baris.
Namun, sebelumnya disarankan sudah mengenal Eliminasi Gauss atau Elimanasi Gauss-Jordan sebab kita akan belajar mereduksi baris pada matriks.
Apa Itu Metode Reduksi Baris ?
Umumnya pada saat kita menghitung determinan dari suatu matriks persegi, kita menggunakan tiga metode pokok yaitu :
- Metode kupu-kupu (Khusus untuk matriks \(2\times2\))

- Metode Sarrus (Khusus untuk matriks \(3\times3\))

- Metode Ekspansi Kofaktor

Selain ketiga metode di atas terdapat metode lain yang dapat digunakan dalam mencari determinan yaitu metode reduksi baris, dimana dalam prosesnya menerapkan operasi baris elementer untuk mengarahkan kedalam bentuk matriks yang sederhana (dapat berupa matriks segitiga, diagonal, eselon baris atau lainnya) tujuannya agar mempermudah dalam menghitung determinannya.
Dalam metode ini tidak ada langkah baku, namun jika kita mengacu pada sifat determinan terutama sifat ke-4 , maka kita punya acuan untuk mereduksi baris sedemikian sehingga terbentuk matriks segitiga.
Menghitung Determinan dengan Metode Reduksi Baris
Perhatikan ilustrasi metode reduksi pada matriks \(3\times 3\) sebagai berikut :

Catatan : Pada ilustrasi di atas, persamaan \(\text{det}(A)=\text{det}(A^{*})=y_{11}\times y_{22}\times y_{33}\) belum tentu benar, namun kita dapat memastikan persamaan tersebut bernilai benar dengan “selalu” menggunakan satu jenis operasi baris elementer, yaitu : menambahkan satu baris dengan kelipatan baris lainnya.
Contoh 11
Tentukan determinan dari matriks \(A\) dengan \(A\) didefinisikan sebagai berikut :
$$A=\left[{\begin{array}{ccc}12&-6&5\\10&11&13\\8&4&-4\end{array}}\right]$$
Penyelesaian :
Pertama-tama kita tuliskan dulu determinan dari \(A\) yakni :
$$\text{det}(A)=\left|{\begin{array}{ccc}12&-6&5\\10&11&13\\8&4&-4\end{array}}\right|$$
Untuk langkah-langkah selanjutnya kita akan menggunakan sifat ke-10.
Sehingga jika kita kenakan operasi \(\frac{1}{4}R_{3}\rightarrow R_{3}\) maka
Ingat, tujuan kita membentuk matriks segitiga (atas atau bawah) sehingga kita sederhanakan baris pertama dan kedua dengan operasi \(-6R_{3}+R_{1}\rightarrow R_{1}\) dan \(-5R_{3}+R_{2}\rightarrow R_{2}\).
Kemudian kita kenakan operasi \(R_{1}\leftrightarrow R_{3}\)
Tidak lupa kita sederhanakan baris ketiga dengan operasi \(2R_{2}+R_{3}\rightarrow R_{3}\) sehingga kita peroleh matriks segitiga.
Nah, setelah ketemu bentuk matriks segitiga, maka berdasarkan sifat ke-4 kita dapatkan :
$$\begin{aligned}-\frac{1}{4}\text{det}(A)&=\left|{\begin{array}{ccc}2&1&-1\\0&6&18\\0&0&47\end{array}}\right|\\&=2\times6\times47\\&=564\\\Leftrightarrow\text{det}(A)&=-4\times564\\&=-2256\end{aligned}$$


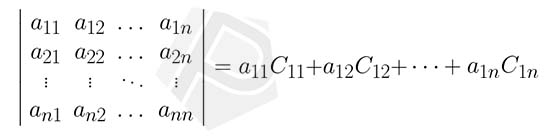



sangat jelas.. sangat membantu..
Iya, semoga bermanfaat.
Bagus….bermanfaat…tetap semangat
Mohon maaf itu untuk yang -1/4 det a bukannya seharusnya dibagi 4 ya, bukan dikali?
maaf izin bertanya, itu pada saat menghitung determninan matriks menggunakan metode reduksi baris digunakan operasi 1/4 R3 , nah setelah itu kok yang dikali det(A) malah 1/4 bukannya ditulis 4.Det(A) untuk hasil akhir si betul dikali 4, tapi apakah pada saat di step seblumnya penulisannya tetep 1/4 .det(a)? tidak 4.det(a) ?
mohon bantuannya ya min 🙂
terima kasih