Berbicara mengenai garis singgung lingkaran, terdapat dua teorema yang mempunyai bentuk persamaan relatif sama.

Teorema paling atas adalah Teorema pitot yang berdasarkan catatan sejarah pertama kali dibuktikan oleh Henri Pitot pada Tahun 1725 melalui memoarnya. Sedangkan dibawahnya adalah Teorema yang diperkenalkan oleh Jacob Steiner dan kita akan mempelajarinya lebih lanjut.
Daftar Isi :
Teorema Steiner pada Garis Singgung Lingkaran

Teorema Steiner berbunyi dalam segiempat garis singgung ABCD (lingkaran di luar) berlaku :
- Jika ABCD segiempat konveks maka AB – CD = AD – BC
- Jika ABCD segiempat konkaf maka AB-CD = AD – BC
- Jika ABCD Segiempat refleks maka AB – CD = BC – AD
Pembuktian
Untuk membuktikannya, pertama kita bagi menjadi tiga kasus :
Kasus 1 (ABCD Segiempat Konveks)
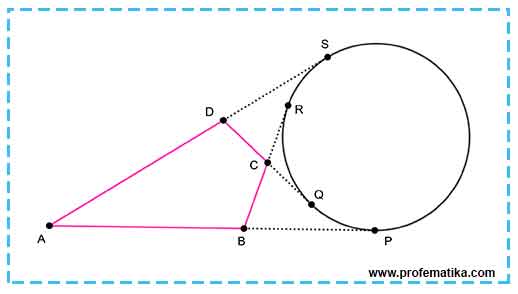
Kita definisikan titik P, Q, R dan S berturut-turut adalah titik singgung pada garis AB, CD, BC dan AD.
Berdasarkan sifat garis singgung pada lingkaran, kita punya :
- AP = AS
- BP = BR
- CQ = CR
- DQ = DS
Kita tahu bahwa
\((AP – BP) – (DQ – CQ) = AB – CD\dots (i)\)
Dilain pihak, dengan mensubstitusikan persamaan (i),(ii),(iii) dan (iv) kita dapatkan :
$$\begin{aligned}(AP-BP)-(DQ-CQ)&= (AS-BR)-(DS-CR)\\&= (AS-DS)-(BR-CR)\\&=AD-BC\dots(ii)\end{aligned}$$
Sehingga dari persamaan (i) dan (ii) diperoleh AB – CD = AD – BC.
Kasus 2 (ABCD Segiempat Konkaf)
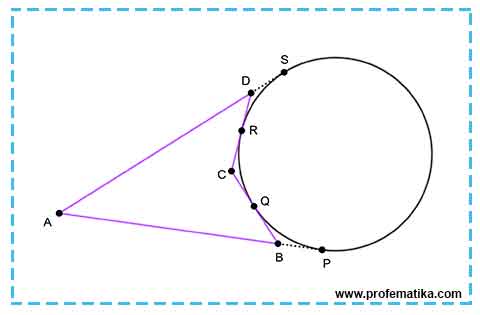
Titik P, Q, R dan S berturut-turut adalah titik singgung pada garis AB, BC, CD dan AD.
Dengan menggunakan sifat garis singgung lingkaran diperoleh :
- AP = AS
- BP = BQ
- CQ = CR
- DR = DS
Kita lakukan operasi persamaan (1) – (2) – (3) -(4) kita punya :
$$\begin{aligned}(AP-BP)-(CR+DR)&= (AS-BQ)-(CQ-DS)\\&=(AS-DS)-(BQ+CQ)\\&=AD-BC\dots(ii)\end{aligned}$$
Jadi didapatkan AB – CD = (AP – BP) – (CR + DR) = AD- BC.
Kasus 3 (ABCD Segiempat Refleks)

Titik P, Q, R dan S berturut-turut adalah titik singgung pada garis AB, AD, BC dan CD.
Masih menggunakan analogi yang sama pada kasus sebelumnya, dimana kita gunakan sifat dasar garis singgung lingkaran sehingga kita peroleh hubungan sebagai berikut :
- AP = AQ
- BP = BR
- CS = CR
- DS = DQ
Sehingga dengan melakukan operasi persamaan ((2) – (1)) – ((4) – (3)) kita dapatkan
$$\begin{aligned}(BP-AP)-(DS-CS)&= (BR-AQ)-(DQ-CR)\\&=(BR+CR)-(AQ+DQ)\\&=BC-AD\dots(ii)\end{aligned}$$
Dilain pihak, kita tahu bahwa (BP – AP) – (DS – CS) = AB – CD
Sehingga AB – CD = BC – AD.
Kesimpulan
Dari kasus 1 sampai kasus 3, dapat disimpulkan bahwa dalam segiempat garis singgung (lingkaran di luar) berlaku selisih panjang sisi yang berhadapan sama dengan selisih pasangan sisi yang berhadapan lainnya. Atau dengan kata lain jika kita punya segiempat garis singgung ABCD (lingkaran diluar) maka berlaku :
- Jika ABCD segiempat konveks maka AB – CD = AD – BC
- Jika ABCD segiempat konkaf maka AB-CD = AD – BC
- Jika ABCD Segiempat refleks maka AB – CD = BC – AD