
Daftar Isi :
Fungsi Determinan / Determinan Matriks
Pada umumnya kita sering melihat fungsi-fungsi seperti \(f(x)=x^2+2x+1\) yang memetakan \((x)\) bilangan real ke bilangan real \(f(x)\). Dari hal tersebut, kemudian para matematikawan mulai melakukan penelitian untuk mencari fungsi yang mengasosiasikan suatu matriks \(X\) dengan bilangan real \(f(x)\). Sehingga munculah fungsi determinan yang nantinya dapat diterapkan dalam mencari invers matriks.
Seki Kowa atau Seki Takakazu adalah matematikawan asal jepang yang pertama kali menemukan determinan, namun masih terbatas pada ordo \(2\times 2\) dan \(3 \times 3\). Akan tetapi muridnya yaitu Laplace berhasil menemukan determinan untuk matriks dengan ordo yang lebih tinggi. Sedangkan istilah “Determinan” pertama kali digunakan oleh Gauss dalam buku berjudul Disquistiones Arithmeticae.
Definisi Fungsi Determinan
Jika \(A\) adalah matriks persegi maka determinan dari matriks \(A\) dapat ditulis \(\text{det}(A)\) atau \(\left|{A}\right|\) yang didefinisikan sebagai jumlahan semua hasil perkalian elementer bertanda dari \(A\).
Lalu apa itu hasil perkalian elementer bertanda?
Eits.. Sebelumnya kita harus mengetahui konsep permutasi terlebih dahulu, karena secara tak langsung merupakan hal penting yang berhubungan dengan hasil perkalian elementer atau bisa dikatakan pondasi dasarnya.
Konsep Permutasi
Pada saat kita duduk dibangku sekolah menengah atas (SMA), kita sudah dikenalkan apa itu permutasi beserta contohnya.
Nah sekarang kita akan sedikit mengulasnya kembali, dimulai dari definisi permutasi hingga pengembangannya.
Baca juga : Konsep Gabungan Matriks Elementer dan OBE untuk Mencari Invers
Definisi 1 (Apa itu permutasi?)
Permutasi dari himpunan bilangan bulat positif \(\{1,2,\dots,n\}\) adalah susunan bilangan-bilangan bulat ini dengan suatu aturan “tanpa menghilangkan” atau “tanpa mengulangi” bilangan-bilangan tersebut.
Contoh 1
Didefinisikan himpunan bilangan-bilangan bulat sebagai berikut :
$$\{1,2,4,5\}$$
Tentukan permutasi dari himpunan di atas?
Penyelesaian :
Ingat tujuan kita adalah mencari susunan berbeda dari bilangan-bilangan bulat pada himpunan di atas tanpa mengulangi dan menghilangkan bilangan-bilangan itu. Salah satu susunannya adalah \((4, 1, 5, 2)\) sedangkan susunan \((2,2,1,5)\) tidak termasuk, karena mengulangi unsur yakni angka \(2\). Lalu bagaimana caranya kita mencari semua susunan yang lainnya?
Untuk mempermudah mencarinya, kita akan menggunakan Pohon Permutasi.
Wah.. semakin menarik ada pohon di matematika. Untuk caranya, perhatikan langkah-langkah berikut :
Langkah 1 :
Kita mulai dari unsur pertama dari kanan yakni angka \(1\). kemudian kita letakkan angka \(1\) di dalam biji pohon.

Langkah 2 :
Unsur atau bilangan selain yang ada didalam lingkaran yaitu \(2, 4\) dan \(5\) (ada \(3\) bilangan maka kita dapat \(3\) cabang baru). Kemudian setiap cabang kita isikan secara berturut-turut angka \(2, 4\) dan \(5\).
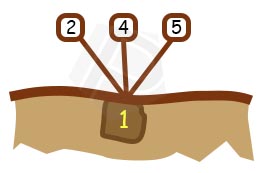
Langkah 3 :
Perhatikan pada cabang pertama (dari kiri) unsur paling atas adalah angka \(2\) sedangkan di bawahnya angka \(1\). Sehingga unsur yang belum ada pada cabang pertama adalah angka \(4\) dan \(5\) (ada \(2\) bilangan maka kita dapat \(2\) anak cabang pada cabang pertama). Kemudian setiap anak cabang pertama kita isikan secara berturut-turut angka \(4\) dan \(5\).

Langkah 4 :
Kita lakukan hal yang sama pada cabang kedua dan ketiga, sehingga kita peroleh :
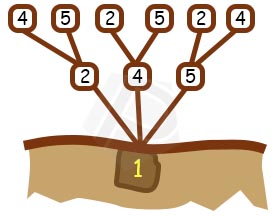
Langkah 5 :
Kita buat anak cabang lagi pada ujung cabang yang sudah ada, dan kenapa harus buat lagi? Kita ambil contoh salah satu cabang (merah), jelas bahwa bilangan yang terhubung dengan cabang merah yakni angka \(1, 2\) dan \(4\) karena permutasi dari \((1,2,4,5)\) terdiri dari \(4\) unsur maka haruslah membuat \(1\) anak cabang lagi pada cabang merah dan pada ujung anak cabang merah kita isikan angka \(5\) (selain \(1, 2\) dan \(4\)). Kemudian tidak lupa kita lakukan hal yang sama pada cabang-cabang lainnya.

Langkah 6 :
Ingat karena himpunan pada soal memiliki \(4\) unsur/bilangan maka juga akan mempunyai \(4\) pohon permutasi. Sehingga dengan menerapkan cara yang sama dari langkah-\(1\) sampai langkah ke-\(4\) kita peroleh \(3\) pohon lainnya.
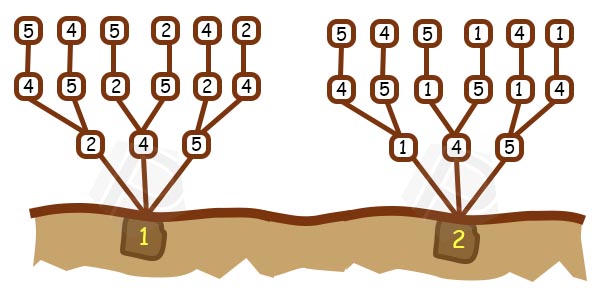

Langkah 7 :
Selanjutnya kita nyatakan setiap ranting pada pohon sebagai suatu susunan, berikut caranya :

Jadi dari 4 pohon kita dapatkan 24 susunan sebagai berikut :
| Pohon ke \(1\) | Pohon ke \(2\) | Pohon ke \(3\) | Pohon ke \(4\) |
| \((1,2,4,5)\) | \((2,1,4,5)\) | \((4,1,2,5)\) | \((5,1,2,4)\) |
| \((1,2,5,4)\) | \((2,1,5,4)\) | \((4,1,5,2)\) | \((5,1,4,2)\) |
| \((1,4,2,5)\) | \((2,4,1,5)\) | \((4,2,1,5)\) | \((5,2,1,4)\) |
| \((1,4,5,2)\) | \((2,4,5,1)\) | \((4,2,5,1)\) | \((5,2,4,1)\) |
| \((1,5,2,4)\) | \((2,5,1,4)\) | \((4,5,1,2)\) | \((5,4,1,2)\) |
| \((1,5,4,2)\) | \((2,5,4,1)\) | \((4,5,2,1)\) | \((5,4,2,1)\) |
Catatan
Pada umumnya terdapat cara praktis untuk mencari “banyaknya permutasi/susunan” dari beberapa unsur dalam suatu himpunan yaitu dengan menggunakan Filling Slot (Metode Pengisian Tempat).
Misalkan terdapat himpunan dengan \(k\) unsur, maka kita dapat mencari banyaknya permutasi dari himpunan tersebut dengan mendefinisikan sebuah “ruang” yang terdiri dari \(k\) slot (ada sebanyak \(k\) bagian) sebagai berikut :
$$\left({\boxed{~^~}_{1},\boxed{~^~}_{2},\dots,\boxed{~^~}_{k}}\right)$$
\(\boxed{~^~}_{i}\) menyatakan banyaknya kemungkinan unsur yang menempati slot/kotak ke-\(i\) dengan \(i=\{1,2,\dots,k\}\). Sehingga kita dapat menghitung banyaknya permutasi dengan rumus :
Kita coba terapkan metode ini untuk mencari banyaknya permutasi pada contoh \(1\) yang mempunyai himpunan \(\{1,2,4,5\}\).
Pertama kita buat ruang dengan \(4\) kotak mengingat himpunan tersebut mempunyai 4 unsur.
$$\left({\boxed{~^~}_{1},\boxed{~^~}_{2},\boxed{~^~}_{3},\boxed{~^~}_{4}}\right)$$
Banyaknya kemungkinan unsur untuk menempati kotak ke-\(1\) ada \(4\) kemungkinan yaitu \(1,2,4\) atau \(5\). Kemudian banyaknya kemungkinan kotak ke-\(2\) ada \(3\) kemungkinan, mengingat satu unsur telah ditempatkan pada kotak ke-\(1\) begitu pula untuk kotak ke-\(3\) dan ke-\(4\) berturut-turut mempunyai \(2\) dan \(1\) kemungkinan, Sehingga kita dapat mencari banyaknya permutasi :
Banyaknya permutasi = \(\boxed{4}_{1}\times\boxed{3}_{2}\times\boxed{2}_{3}\times\boxed{1}_{4}=24\) buah.
Baca juga :Definisi Matriks Elementer dan Sifatnya
Definisi 2 (Apa itu inversi?)
Misalkan didefinisikan \((p_{1}, p_{2},\dots,p_{k})\) sebagai permutasi dari himpunan dengan \(k\) unsur bilangan bulat. Contohnya jika kita punya himpunan \(\{1,2,3\}\) maka salah satu permutasinya adalah \((3,1,2)\) dengan \(p_{1}=3, p_{2}=1\) dan \(p_{3}=2\).
Dalam permutasi \((p_{1}, p_{2},\dots,p_{k})\), dikatakan terjadi sebuah inversi (inversion) apabila sebuah bilangan bulat yang lebih besar mendahului sebuah bilangan bulat yang lebih kecil, atau dapat kita katakan terjadi inversi jika terdapat \(p_{i}>p_{j}\) dengan \(i<j\) dan \(i,j \in \{1,2,\dots,k\}\).
Contoh 2
Tentukan banyaknya inversi dalam permutasi \((4,1,2,0,5)\) ?
Penyelesaian :
Pertama kita cermati banyaknya bilangan bulat yang lebih kecil daripada \(p_{1} = 4\), dapat kita lihat jelas terdapat \(3\) bilangan yang lebih kecil yakni \(p_{2}=1, p_{3}=2\) dan \(p_{4}=0\).
Langkah kedua kita lakukan hal yang sama untuk \(p_{2}=1, p_{3}=2, p_{4}=0\) dan \(p_{5}=5\), kemudian jumlahkan seluruh inversinya. Lebih jelasnya perhatikan tabel berikut :
| Unsur | Lebih Besar Dari | Jumlah |
| \(p_{1}=4\) | \(p_{2}, p_{3}, p_{4}\) | 4 |
| \(p_{2}=1\) | \(p_{4}\) | 1 |
| \(p_{3}=2\) | \(p_{4}\) | 1 |
| \(p_{4}=0\) | Tidak ada | 0 |
| \(p_{5}=5\) | Tidak ada | 0 |
| Banyaknya Inversi | 6 |
Definisi 3 (Permutasi Genap dan Ganjil)
Sebuah permutasi \((p_{1}, p_{2},\dots,p_{k})\) dinamakan permutasi genap (even) jika jumlah inversi dalam permutasi tersebut genap. Sebaliknya, sebuah permutasi dinamakan ganjil (odd) jika jumlah inversi dalam permutasi tersebut ganjil.
Contoh 3
Permutasi \((2,5,0,3)\) adalah permutasi ganjil karena banyaknya inversi \(1 + 2 + 0 + 0 = 3\) (ganjil)
Definisi Hasil Perkalian Elementer
A matriks persegi \(n \times n\) dan kita tuliskan sebagai berikut:
$$A=\left[{\begin{array}{cccc}a_{11}&a_{12}&\dots&a_{1n}\\a_{21}&a_{22}&\dots&a_{2n}\\\vdots&\vdots&\ddots&\vdots\\a_{n1}&a_{n2}&\dots&a_{nn}\end{array}}\right]$$
Maka hasil perkalian elementer dari matriks A adalah hasil perkalian elemen-elemen pada A yang letaknya sebaris atau sekolom. Semisal \(A=[a_{ij}]_{3 \times 3}\) maka salah satu hasil perkalian elementernya yaitu \(a_{12}a_{23}a_{32}\).
Lalu bagaimana cara mencari semua hasil perkalian elementer?
Untuk lebih jelasnya simak contoh berikut :
Contoh 4
Didefinisikan matriks persegi \(A\) dengan ordo \(3 \times 3\) sebagai berikut :
$$A=\left[{\begin{array}{ccc}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{array}}\right]$$
Tentukan semua hasil perkalian elementernya.
Penyelesaian :
Karena matriks A mempunyai ordo \(3 \times 3\) maka kita tuliskan bentuk acuan perkalian elementernya sebagai perkalian \(3\) elemen pada matriks A yakni \(a_{1p_{1}}a_{2p_{2}}a_{3p_{3}}\). Kemudian kita ganti tanda \(p_{1}, p_{2}\) dan \(p_{3}\) dengan seluruh permutasi dari \((1,2,3)\). Kenapa 1, 2 dan 3? karena kotak \(p_{1}, p_{2}\) dan \(p_{3}\) mewakili urutan kolom dan banyaknya kolom pada matriks A ada \(3\), yaitu kolom ke-\(1, 2\) dan \(3\). Untuk lebih jelasnya perhatikan tabel di bawah ini :
| Permutasi \((1,2,3)\) | Ubah \(a_{1p_{1}}a_{2p_{2}}a_{3p_{3}}\) |
| \((1,2,3)\) | \(a_{11}a_{22}a_{33}\) |
| \((1,3,2)\) | \(a_{11}a_{23}a_{32}\) |
| \((2,1,3)\) | \(a_{12}a_{21}a_{33}\) |
| \((2,3,1)\) | \(a_{12}a_{23}a_{31}\) |
| \((3,1,2)\) | \(a_{13}a_{21}a_{32}\) |
| \((3,2,1)\) | \(a_{13}a_{22}a_{31}\) |
Catatan
Apabila matriks \(A\) berordo \(n\times n\), maka seluruh hasil perkalian elementer dalam matriks ada sebanyak \(n!\). Karena banyaknya hasil kali elementer sama dengan banyaknya permutasi dari \((p_{1}, p_{2},\dots,p_{n})\) yaitu dengan menggunakan metode filling slot didapat banyaknya permutasi = \(n(n-1)\dots (2)(1)= n!\).
Baca juga : Sistem Persamaan Linear Homogen dan Sifatnya
Hasil Perkalian Elementer Bertanda untuk Mencari Determinan
Sedikit berbeda dari sebelumnya, hasil perkalian elementer bertanda dari matriks \(A\) persegi yang berordo \(n \times n\) adalah hasil perkalian elementer \(a_{1p_{1}}a_{2p_{2}}\dots a_{np_{n}}\) yang dikalikan dengan \(+1\) jika permutasinya genap dan dikalikan dengan \(-1\) jika permutasinya ganjil.
Contoh 5
Berdasarkan contoh \(4\) tentukan semua hasil perkalian elementer bertandanya.
Penyelesaian :
Untuk mempermudah mencari hasil perkalian elementer bertanda, kita kembangkan tabel pada contoh \(4\) sehingga :
| Permutasi | Inversi | Hasil Perkalian Elementer Bertanda |
| \((1,2,3)\) | 0 | \(+a_{11}a_{22}a_{33}\) |
| \((1,3,2)\) | 1 | \(-a_{11}a_{23}a_{32}\) |
| \((2,1,3)\) | 1 | \(-a_{12}a_{21}a_{33}\) |
| \((2,3,1)\) | 2 | \(+a_{12}a_{23}a_{31}\) |
| \((3,1,2)\) | 2 | \(+a_{13}a_{21}a_{32}\) |
| \((3,2,1)\) | 3 | \(-a_{13}a_{22}a_{31}\) |
Lalu apa hubungannya dengan fungsi determinan?
Jadi jika \(A\) adalah matriks persegi yang berordo \(n\times n\) maka Determinan/Fungsi Determinan didefinisikan sebagai jumlahan semua hasil perkalian elementer bertanda dari matriks \(A\). Atau bisa ditulis :
$$\text{det}(A)=\sum \pm a_{1p_{1}}a_{2p_{2}}\dots a_{np_{n}}$$
Contoh 6
Diberikan matriks \(A\) sebagai berikut :
$$A=\left[{\begin{array}{ccc}-1&1&0\\0&2&1\\2&-2&-1\end{array}}\right]$$
Tentukan determinan dari matriks \(A\) tersebut.
Penyelesaian :
Berhubung pada contoh 5, matriks A berordo \(3 \times 3\) sudah dicari semua hasil perkalian elementer bertandanya maka kita peroleh :
$$\text{det}(A)=\sum \pm a_{1p_{1}}a_{2p_{2}}a_{3p_{3}}$$
Sebenarnya terdapat metode yang lebih praktis dalam mencari determinan matriks \(A\), yaitu dengan Metode Sarrus.





sangat menarik
Terima kasih sudah berkunjung, semoga bermanfaat