Daftar Isi :
Definisi Sistem Persamaan Linear Homogen
Suatu sistem persamaan linear disebut homogen jika konstantanya bernilai 0. Disini kita membedakan konstanta dan koefisien, dimana konstanta pada umumnya berada pada ruas kanan persamaan sedangkan koefisien “berdampingan” dengan variabel.
Pada umumnya suatu sistem persamaan linear dapat dituliskan :
$$\vdots$$
Dengan \(a_{ij}\) menyatakan koefisien, \(x_{j}\) menyatakan variabel dan \(b_{i}\)menyatakan konstanta untuk setiap \(i=\{1,2,3,\dots,m\}~\text{dan}~j=\{1,2,3,\dots,n\}\). SPL tersebut dinyatakan homogen jika \(b_{i}=0\) atau dapat ditulis kembali :
$$\vdots$$
Contoh 1 :
$$5x_{1} -2x_{2} +x_{3} -3x_{4}=0$$
$$2x_{1} + x_{2} -x_{3} -7x_{4}=0$$
$$2x_{2} – 3x_{3} =0$$
$$3x_{2} +4x_{3} +x_{4}=0$$
Bisakah anda mencari solusi dari SPL diatas tanpa menggunakan metode Operasi Baris Elementer ?
Contoh 2 :
$$3x+y-z=0$$
$$5x-2y+z=0$$
$$2x+3y+2=0$$
Pada contoh kedua, sistem tersebut tidak bersifat homogen, sebab jika kita perhatikan pada persamaan ketiga terdapat konstanta yang bernilai tidak nol melainkan bernilai 2.
Teorema 1 (Sistem Persamaan Linear Homogen bersifat Konsisten)
Suatu sistem persamaan linear homogen bersifat konsisten karena terdapat satu solusi yang diperoleh dengan mengatur setiap variabel bernilai nol.
Bukti :
Atur setiap variabel bernilai nol, maka ketika kita menggantikan nilai variabel pada setiap persamaan, maka ruas kiri akan menghasilkan nol, tak peduli apapun koefisiennya. Kemudian karena sistem persamaan linear homogen mempunyai konstanta di ruas kanan bernilai nol akibatnya setiap persamaan bernilai benar dan karena setidaknya mempunyai satu solusi (semua variabel bernilai nol) maka sistem persamaan linear homogen bersifat konsisten.
Definisi Solusi Trivial dalam SPL Homogen
Dikutip dari halaman wikipedia arti kata trivial merupakan hal yang sepele, biasa dan tidak penting. Jadi dapat dikatakan solusi trivial merupakan solusi yang “biasa-biasa saja” bukan hal yang istimewa.
Definisi :
Misalkan terdapat sistem persamaan linear homogen dengan \(n\) variabel. Maka solusi dengan \(x_{1}=0,~x_{2}=0,~x_{3}=0,\dots,x_{n}=0\) disebut juga solusi trivial.
Teorema 2 (SPL Homogen dengan Variabel > Persamaan)
Misalkan terdapat suatu persamaan linear homogen mempunyai \(m\) persamaan dan \(n\) variabel dengan \(n > m\). Maka sistem tersebut mempunyai tak hingga banyaknya solusi.
Untuk bukti lengkapnya anda bisa baca di : http://linear.ups.edu/html/section-HSE.html
Contoh dari teorema 2 :
\(2x +3y +4z =0\)
\(3x -2z =0\)
Dari sistem di atas terdapat 2 persamaan dan 3 variabel. Selanjutnya kita akan mengecek apakah benar sistem tersebut mempunyai tak hingga banyaknya solusi ?
Kita akan mengeceknya menggunakan metode eliminasi gauss-jordan dengan Operasi Baris Elementer.
Langkah 1
Kita representasikan kedalam bentuk matriks :
$$\left[{\begin{array}{ccc}2&3&4\\3&0&-2\end{array}}\right|\left.{\begin{array}{c}0\\0\end{array}}\right]$$
Langkah 2
Kita buat 1 utama pada baris pertama dengan operasi \(\frac{1}{2}R_{1} \rightarrow R_{1}\), sehingga kita peroleh :
Langkah 3
Kita sederhanakan baris kedua dengan operasi \(-3R_{1} +R_{2} \rightarrow R_{2}\) dan didapat :
Langkah 4
Kita buat 1 utama pada baris kedua dengan operasi \(-\frac{2}{9}R_{2} \rightarrow R_{2}\)
Pada bentuk akhir pada langkah ini disebut juga bentuk eselon baris. Kita akan menyederhanakannya lagi sehingga menjadi bentuk eselon baris tereduksi.
Langkah 5
Selanjutnya kita sederhanakan lagi bentuk baris pertama dengan operasi \(-\frac{3}{2}R_{2} +R_{1} \rightarrow R_{1}\) dan diperoleh :
Bentuk akhir pada langkah ke lima merupakan bentuk eselon baris tereduksi. kemudian kita ubah lagi kebentuk sistem persamaan linear :
Persamaan \((i)\) dan \((ii)\) dapat pula dituliskan sebagai :
$$x=\frac{2}{3}z$$
$$y=-\frac{16}{9}z$$
Sehingga jika kita tetapkan \(z = k\) untuk sebarang bilangan \(k\) maka diperoleh himpunan penyelesaian sebagai berikut :
atau
Jelas dengan melihat himpunan penyelesaian di atas, sistem persamaan linear homogen pada soal mempunyai tak hingga banyaknya solusi.
Grafik SPL Homogen
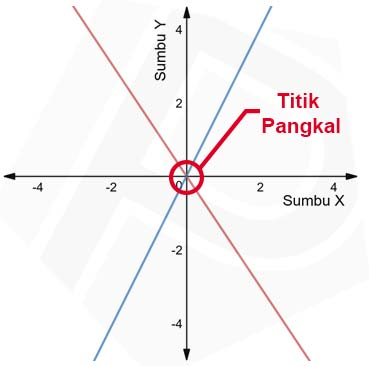
Suatu sistem persamaan linear homogen mempunyai solusi trivial sehingga apabila setiap persamaanya dilukiskan kedalam suatu grafik maka grafiknya akan melewati titik pangkal (titik asal atau titik koordinat kartesius).
Catatan : SPL 2 variabel grafiknya berupa garis-garis, SPL 3 variabel grafiknya berupa bidang-bidang sedangkan untuk SPL dengan variabel lebih dari 3 belum memungkinkan untuk dilukiskan.
Contoh :
Diberikan SPL homogen 2 variabel sebagai berikut :
$$\color{red}{3x+2y=0}$$
$$\color{blue}{2x-y=0}$$
Grafiknya :
 Contoh 2 :
Contoh 2 :
Diberikan SPL homogen 3 variabel sebagai berikut :
$$\color{red}{4x-2y+3z=0}$$
$$\color{blue}{2x-y-5z=0}$$
$$\color{green}{3x+2y-2z=0}$$
Grafiknya :

Kesimpulan
- SPL homogen mempunyai ciri khas yaitu konstanta-konstantanya bernilai nol.
- Sistem persamaan linear homogen bersifat konsisten, selalu mempunyai solusi setidaknya satu solusi (solusi trivial).
- SPL Homogen dengan banyak variabel \(>\) banyak persamaan, maka sistem tersebut mempunyai tak hingga banyaknya solusi.




kak, gimana kalau SPL Homogen dengan Persamaan > Variabel?? Pasti memiliki baris nol kan??