Daftar Isi :
Definisi Determinan Secara Umum
Pada pembahasan sebelumnya sudah dijelaskan dengan jelas mengenai Definisi Fungsi Determinan dengan Perkalian Elementer. Dimana jika terdapat \(A\) matriks persegi berordo \(n\times n\) maka determinan dari matriks \(A\) dapat ditulis sebagai berikut :
$$\text{det}(A)=\sum \pm a_{1p_{1}}a_{2p_{2}}\dots a_{np_{n}}$$
Dengan \(a_{1p_{1}}a_{2p_{2}}\dots a_{np_{n}}\) bernilai genap jika \((p_{1},p_{2},\dots,p_{n})\) merupakan permutasi genap, sebaliknya \(a_{1p_{1}}a_{2p_{2}}\dots a_{np_{n}}\) bernilai ganjil jika \((p_{1},p_{2},\dots,p_{n})\) merupakan permutasi ganjil. Ingat kembali bahwa permutasi dari \(n\) unsur berbeda dari \((p_{1},p_{2},\dots,p_{n})\) mempunyai \(n!\) permutasi.
Kita akan menggunakan definisi fungsi determinan dengan perkalian elementer untuk melihat apakah metode sarrus hanya berlaku pada matriks \(3\times3\). Sebelum menganalisa lebih lanjut, mari kita kenalan terlebih dahulu metode sarrus.
Apa itu aturan atau metode sarrus?
Metode sarrus atau juga sering orang menyebutnya metode anyaman (Basketweave Method) adalah jalan alternatif dalam menghitung determinan dari matriks \(3\times 3\).
Perhatikan ilustrasi berikut :

Berdasarkan ilustrasi di atas kita peroleh langkah-langkah menghitung determinan matriks \(3\times 3\) dengan metode sarrus sebagai berikut.
Tahapan Metode Sarrus dalam Mencari Determinan
Misalkan didefinisikan matriks \(A_{3\times 3}\) sebagai berikut :
$$A=\left[{\begin{array}{ccc}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{array}}\right]$$
Langkah pertama dalam menentukan determinan dengan aturan sarrus yaitu dengan menambahkan secara berurutan kolom ke-\(1\) dan ke-\(2\) pada sebelah kanan kolom ke-\(3\).
$$\left[{\begin{array}{ccc|cc}a_{11}&a_{12}&a_{13}&a_{11}&a_{12}\\a_{21}&a_{22}&a_{23}&a_{21}&a_{22}\\a_{31}&a_{32}&a_{33}&a_{31}&a_{32}\end{array}}\right]$$
Selanjutnya kita coret entri-entri pada diagonal utama dan diagonal lainnya.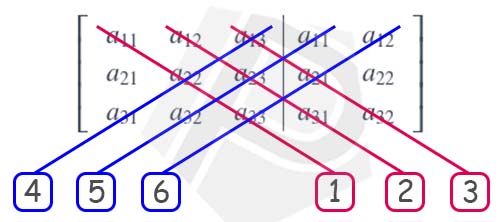
Sehingga diperoleh 6 bagian, kemudian kita kalikan entri-entri yang terletak pada kotak 1 sampai kotak 6.
$$\boxed{1}=a_{11}\times a_{22}\times a_{33}$$
$$\boxed{2}=a_{12}\times a_{23}\times a_{31}$$
$$\boxed{3}=a_{13}\times a_{21}\times a_{32}$$
$$\boxed{4}=a_{13}\times a_{22}\times a_{31}$$
$$\boxed{5}=a_{11}\times a_{23}\times a_{32}$$
$$\boxed{6}=a_{12}\times a_{21}\times a_{33}$$
Langkah terakhir yaitu menghitung determinan dengan mengurangkan jumlah hasil kali pada diagonal-diagonal utama(kotak 1, kotak 2 dan kotak 3) dengan jumlah hasil kali pada diagonal-diagonal pelengkapnya(kotak 4, kotak 5 dan kotak 6).
Baca juga : Kelebihan dan Kekurangan Metode Ekspansi Kofaktor
Menghitung Determinan Matriks 3×3 dengan Aturan Sarrus
Diberikan matriks \(A_{3\times 3}\) sebagai berikut :
$$A=\left[{\begin{array}{ccc}2&-1&1\\-3&0&-2\\1&4&1\end{array}}\right]$$
Dengan menggunakan aturan sarrus, tentukan determinan matriks \(A\) tersebut.
Penyelesaian :
Berdasarkan aturan sarrus maka kita peroleh :
$$\left[{\begin{array}{ccc|cc}2&-1&1&2&-1\\-3&0&-2&-3&0\\1&4&1&1&4\end{array}}\right]$$

Sehingga determinan dari matriks \(A\) yaitu :
Alasan Metode Sarrus Hanya Berlaku Pada Matriks 3×3
Sebenarnya mengenai alasan aturan sarrus hanya berlaku pada matriks 3×3 tidak perlu ditanyakan, mengapa?
Hal ini karena Metode Sarrus itu sendiri diciptakan sebagai jalan alternatif yang lebih mudah untuk menghitung determinan matriks 3×3.
Namun, penulis mempunyai pandangan yang sedikit berbeda mengenai hal tersebut. Pertama kita sepakati bersama bahwa dalam mencari determinan matriks \(A_{n\times n}\) dengan metode sarrus pada diskusi kita kali ini dimulai dengan menambahkan \(n-1\) kolom pertama tepat pada sebelah kanan kolom terakhir secara berturut-turut.
Ide tersebut terinspirasi pada aturan sarrus pada matriks \(3\times 3\) dimana tepat pada sebalah kanan kolom terakhir (ketiga), terdapat \(3-1\) kolom pertama (kolom ke-\(1\) dan kolom ke-\(2\) secara berturut-turut).
Sehingga jika kita hubungkan pada konsep hasil perkalian elementer maka kita akan mendapatkan \(2n\) buah hasil perkalian elementer. Contohnya pada matriks \(3 \times 3\) berdasarkan aturan sarrus maka akan terdapat \(2\times3=6\) buah hasil kali elementer (3 pada diagonal utama dan 3 lainnya pada diagonal pelengkapnya).
Namun, jika kita mengacu pada definisi determinan dengan hasil perkalian elementer maka apabila matriks \(A\) berordo \(n\times n\), maka seluruh hasil perkalian elementer dalam matriks ada sebanyak \(n!\) (baca sebabnya disini).
Sehingga dari kedua pernyataan di atas kita peroleh hubungan :
$$n!=2n$$
Jelas bahwa jika bilangan asli \(n>3\) maka $$n!>2n$$ (kontradiksi) yang berakibat \(1\leq n\leq 3\) dan nilai \(n\) yang memenuhi persamaan tersebut hanya \(n=3\).
Jadi dari pernyataan di atas dapat kita tarik kesimpulan bahwa aturan sarrus hanya berlaku untuk matriks berordo \(3\times 3\).