Daftar Isi :
Operasi Matriks
Operasi dasar seperti penjumlahan dan perkalian erat sekali berhubungan dengan matriks. Namun, operasi tersebut tidak selalu dapat langsung diterapkan, karena matriks lebih rumit daripada angka.
1. Penjumlahan Matriks
Jika terdapat dua matriks yang mempunyai banyak baris dan kolom yang sama, maka kita dapat menjumlahkan keduanya untuk memperoleh matriks baru dengan ordo yang sama. Jadi syarat untuk menjumlahkan dua matriks atau lebih yaitu harus mempunyai ordo yang sama.
Misalkan matriks \(A\) dan \(B\) mempunyai ordo \(m \times n\) atau dapat ditulis \(A=[a_{ij}]_{m \times n}~,~B=[b_{ij}]_{m \times n}\) dengan \(i=\{ 1,2,\dots,m\}\) dan \(j=\{1,2,\dots,n\}\). Jika kedua matriks tersebut dijumlahkan maka akan terdapat matriks \(C=[c_{ij}]_{m \times n}\), dimana \(C=A+B\) dengan \(c_{ij}=a_{ij}+b_{ij}\).
Contoh :
Misalkan matriks \(A\) dan \(B\) didefinisikan sebagai berikut.
Kita akan mencari matriks \(C\) dengan menjumlahkan matriks \(A\) dan \(B\). Sehingga kita peroleh :
Selain menjumlahkan kita juga bisa menggunakan operasi pengurangan dengan syarat harus mempunyai ordo yang sama. Untuk contohnya kita dapat menghitung :
Lalu bagaimana jika terdapat dua matriks mempunyai ordo yang berbeda kemudian keduanya dijumlahkan? Misalkan terdapat matriks \(D\) dengan ordo \(2 \times 3\). Jika ditanya \(A+D\) maka \(A+D=~\text{tidak terdefinisi}\) karena \(\text{ordo}~A\neq~\text{ordo}~D\).
2. Perkalian dengan Skalar
Misalkan matriks \(A=[a_{ij}]_{m \times n}\) dan \(\alpha\) adalah sembarang skalar (riil atau kompleks). Perkalian matriks \(A\) dengan skalar \(\alpha\) dapat dibentuk dengan mengalikan setiap elemen \(a_{ij}\) dengan \(\alpha\).
Contoh :
Misalkan \(\alpha=2~,~\beta = 1+2i\) dan matriks \(A\) didefinisikan sebagai berikut.
Tentukan hasil dari \(\alpha A\) dan \(\beta B\).
Penyelesaian :
Kita dapat menyelesaikannya dengan mengalikan skalar dengan setiap elemen pada matriks \(A\). Sehingga untuk \(\alpha A\) kita peroleh :
Dengan cara yang sama, kita juga dapat :
3. Perkalian Dua Matriks
Pada operasi dua matriks, pertama-tama kita akan mempelajari perkalian antara vektor kolom dan vektor baris. Hal tersebut karena berkaitan langsung dan menjadi landasan dalam perkalian antar matriks.
Apa itu vektor kolom dan vektor baris?
Vektor Kolom adalah matriks yang memiliki ordo \(n \times 1\) dengan elemen sebanyak \(n\). Contoh :
Vektor Baris adalah matriks yang memiliki ordo \(1 \times n\) dengan elemen sebanyak \(n\). Contoh :
Perkalian Vektor Kolom dan Vektor Baris
Selanjutnya untuk perkalian antar vektor kolom dan vektor baris, kita misalkan \(A=[a_{i}]_{1 \times n}\) dan \(B=[b_{i}]_{n \times 1}\) berturut-turut merupakan vektor baris dan kolom dengan \(n\) elemen dan \(i=\{1,2,\dots,n\}\). Jika kedua matriks tersebut dikalikan maka diperoleh :
Keunikan dari perkalian antar vektor kolom dan baris yaitu hasilnya berupa bilangan bukan matriks. Kemudian perkalian tersebut dapat terjadi (valid) jika dan hanya jika mempunyai banyak elemen yang sama.
Contoh :
Misalkan matriks \(A~,~B~,~C\) didefinisikan sebagai berikut.
Tentukan hasil dari \(AC\) dan \(BC\).
Penyelesaian :
Dengan menggunakan rumus sebelumnya maka diperoleh :
Untuk perkalian \(BC=tidak~terdefinisi\) karena banyak elemen \(B\) tidak sama dengan banyak elemen \(C\).
Perkalian Antar Matriks Secara Umum
Setelah berhasil mempelajari perkalian antara vektor baris dan vektor kolom. Selanjutnya kita akan mempelajari perkalian antara dua matriks sembarang ukuran beserta ketentuannya.
Misalkan terdapat dua matriks yaitu \(A=[a_{ij}]_{l \times m}\) dan \(B=[b_{ij}]_{m \times n}\). Misalkan lagi terdapat matriks \(C\) dengan \(C=AB\). Maka kita dapat menuliskan setiap elemen dari \(C\) sebagai berikut.
Jika hal tersebut dikaitkan dengan vektor kolom dan vektor baris, maka jika didefinisikan \(a_{i}\) dan \(b_{j}\) berturut-turut merupakan vektor baris ke-\(i\) dari matriks \(A\) dan vektor kolom ke-\(j\) dari matriks \(B\). Maka elemen dari \(C\) dapat juga ditulis \(c_{ij}=a_{i}b_{j}\).
Jadi berdasarkan pernyataan-pernyataan tersebut dapat ditarik kesimpulan, perkalian dua matriks (\(AB\)) dapat terjadi (valid) jika dan hanya jika banyak kolom \(A=\) banyak baris \(B\).
Contoh :
Didefinisikan matriks \(A\) dan \(B\) sebagai berikut.
Tentukan hasil dari \(AB\) dan \(BA\).
Penyelesaian :
Langkah pertama, untuk \(AB\) kita harus mengecek banyak kolom \(A\) dan banyak baris \(B\). Jelas bahwa banyak kolom \(A=\) banyak baris \(B=3\) sehingga dapat dilakukan operasi perkalian.
Sedangkan untuk \(BA\) dengan langkah yang sama didapat bahwa banyak kolom \(B=3\) tidak sama dengan banyak baris \(A=2\) akibatnya tidak terdefinisi atau operasi perkalian tersebut tidak dapat dilakukan.
Langkah kedua, untuk memudahkan penulisan misalkan terdapat matriks \(C=AB\). Sehingga berdasarkan pernyataan sebelumnya, elemen dari matriks \(C\) yaitu \(c_{ij}=a_{i}b_{j}\).
Langkah ketiga, kita dapat memulai menghitung dengan mengalikan matriks vektor baris ke-\(1 = a_{1}\)(dari matriks \(A\)) dengan vektor kolom ke-\(1 =b_{1}\)(dari matriks \(B\)).
Dengan langkah yang sama akan dicari elemen-elemen dari matriks \(C\) yang lain \(\{c_{11},c_{12},c_{13},c_{21},c_{22},c_{23}\}\).
Sehingga diperoleh :
Dari contoh tersebut didapat fakta bahwa jika \(A\) mempunyai ordo \(m \times k\) dan \(B\)mempunyai ordo \(k \times n\) maka \(C=AB\) mempunyai ordo \(m \times n\).
4. Transpose Matriks
Transpose matriks adalah matriks yang dibentuk dengan mempertukarkan elemen-elemen didalam baris dan kolom dari matriks tersebut. Umumnya disimbolkan dengan transpose \(A=A^T\).
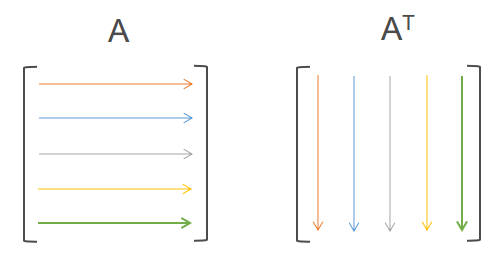
Misalkan matriks \(A=[a_{ij}]_{m \times n}\) dan transpose matriks A dinyatakan oleh \(A^T=B=[b_{ij}]_{n \times m}\) maka berdasarkan definisi \(b_{ij}=a_{ji}\) dan perlu diperhatikan bahwa jika ordo matriks \(A = m \times n\) maka ordo \(A^T = n \times m \).
Contoh :
Misalkan matriks \(A\) dan \(B\) didefinisikan sebagai berikut.
Maka matriks transpose dari \(A\) dan \(B\) yaitu :
5. Trace Matriks
Trace Matriks dari matriks persegi adalah hasil penjumlahan dari elemen-elemen pada diagonal utama matriks tersebut. Jadi syarat untuk mencari trace matriks yaitu matriksnya mempunyai ordo \(n \times n\) (matriks persegi). Untuk penulisan biasa disimbolkan dengan trace\(A)=tr(A)\).
Misalkan \(A=[a_{ij}]_{n \times n}\), maka berdasarkan definisi diperoleh :
Contoh :
Misalkan didefinisikan sebuah matriks persegi sebagai berikut.
$$A=\left[{\begin{array}{ccc}2&3&1\\-2&-7&4\\5&6&-2\end{array}}\right]$$
Maka \(tr(A)=a_{11}+a_{22}+a_{33}=2+(-7)+(-2)=-7\)
Sifat-Sifat Operasi Matriks
Catatan : Pada pembahasan sifat-sifat operasi kali ini dapat dilakukan dengan menganggap bahwa ukuran-ukuran matriks yang dioperasikan disesuaikan dengan ketentuan dari setiap operasi.
1. Terhadap Operasi Penjumlahan
Misalkan terdapat matriks \(A, B, C\) dan matriks nol \(O\) sedemikian rupa sehingga berlaku :
- \(A+B=B+A\)
- \(A+(B+C)=(A+B)+C\)
- \(A+O =O+A=A\)
- \(A+(-A)=-A+A=O\)
2. Terhadap Operasi Perkalian
Misalkan terdapat matriks \(A, B, C,\) matriks nol \(O,\) matriks identitas \(I\) dan \(m,n\) sembarang bilangan bulat yang sedemikian rupa sehingga berlaku :
- \(AB\neq BA\)
- \((AB)C=A(BC)\)
- \(AI=IA=A\)
- \(AO=OA=O\)
- \(A^m A^n=A^{m+n}~\text{dan}~(A^m)^n=A^{mn}\)
- \(A^x=\begin{cases}I & \text{ jika } x= 0\\\underbrace{AA\dots A}_{x~faktor}& \text{ jika } x\in \mathbb{N}\end{cases}\)
- \(\text{jika matriks diagonal}~A_{n \times n}=\left[{\begin{array}{cccc}a_{11}&0&\dots&0\\0&a_{22}&\dots&0\\\vdots&\vdots&\ddots&\vdots\\0&0&\dots&a_{nn}\end{array}}\right],~\text{maka}~A^k=\left[{\begin{array}{cccc}(a_{11})^k&0&\dots&0\\0&(a_{22})^k&\dots&0\\\vdots&\vdots&\ddots&\vdots\\0&0&\dots&(a_{nn})^k\end{array}}\right]\)
- \(\text{jika}~AB=O~\text{maka tidak selalu}~A=O~\text{atau}~B=O~\text{atau}~BA=O\)
3. Terhadap Penjumlahan dan Perkalian dengan Skalar
Misalkan terdapat matriks \(A, B, C,\) dan \(m,n\) sembarang skalar (riil atau kompleks) yang sedemikian rupa sehingga berlaku :
- \(A(B+C)=AB+AC\)
- \((B+C)A=BA+CA\)
- \(m(A+B)=mA+mB\)
- \((m+n)A=mA+nA\)
- \((mn)A=m(nA)\)
- \(m(BC)=(mB)C=B(mC)\)
4. Terhadap Operasi Transpose
Misalkan terdapat matriks \(A, B, \) dan \(\alpha\) sembarang skalar (riil atau kompleks) yang sedemikian rupa sehingga berlaku :
- \((A+B)^T=A^T+B^T\)
- \((\alpha A)^T=\alpha A^T\)
- \((A^T)^T=A\)
- \((AB)^T=B^T A^T\)
5. Terhadap Operasi Trace
Misalkan terdapat matriks \(A, B, I\text{(Identitas)}\) dan \(\alpha\) sembarang skalar (riil atau kompleks) dan sembarang bilangan bulat \(n\) yang sedemikian rupa sehingga berlaku :
- \(tr(\alpha A)=\alpha (tr(A))\)
- \(tr(A+B) = tr(A)+tr(B)\)
- \(tr(AB)=tr(BA)\)
- \(tr(A^T)=tr(A)\)
- \(tr(I_{n \times n})= n\)