Pemecahan SPL dengan Operasi Baris Elementer

Pemecahan SPL dengan Operasi Baris Elementer

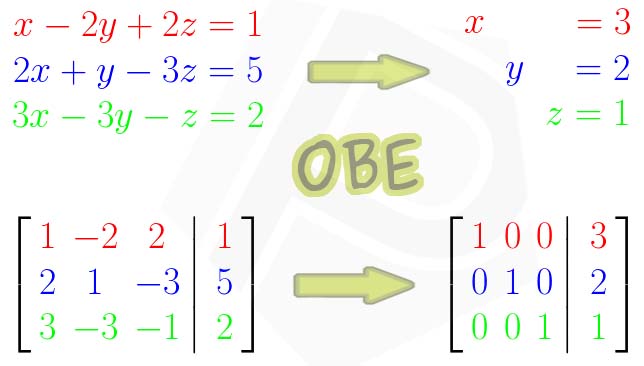
Ilustrasi di atas menunjukkan tujuan pemecahan dengan OBE yaitu membentuk sistem baru atau merubah matriks kedalam salah satu bentuk yang paling sederhana agar mudah dipecahkan. Perlu diketahui dalam proses perubahan tersebut, mempunyai urutan operasi yang bermacam-macam, sehingga memungkin juga diperoleh sistem/matriks yang berbeda, namun mempunyai himpuan penyelesaian yang sama.

Disarankan sudah membaca :Pengenalan Operasi Baris Elementer

Contoh 1 (Solusi Tunggal)

Diberikan sistem persamaan linear sebagai berikut :

\(\color{red}{L_{1}~:~3x -y +z=4}\)
\(\color{blue}{L_{2}~:~-2x+2y +3z  =11}\)
\(\color{green}{L_{3}~:~x +3y -2z=1}\)

Carilah pemecahan sistem persamaan linear tersebut dengan operasi baris elementer.

Penyelesaian :

Pertama kita representasikan sistem persamaan linear tersebut ke dalam bentuk matriks :

$$\left[{\begin{array}{ccc} \color{red}{3}&\color{red}{-1}&\color{red}{1}\\\color{blue}{-2}&\color{blue}{2}&\color{blue}{3}\\\color{green}{1}&\color{green}{3}&\color{green}{-2}\end{array}}\right|\left.{\begin{array}{c}\color{red}{4}\\\color{blue}{11}\\\color{green}{1}\end{array}}\right]$$

Perhatikan ilustrasi perubahan bentuk matriks berikut, yang dapat dijadikan acuan untuk menetukan langkah-langkah operasinya :

Langkah 1

Untuk mempermudah kita akan membentuk menjadi :

$$\left[{\begin{array}{ccc}1&?&?\\?&?&?\\?&?&?\end{array}}\right|\left.{\begin{array}{c}?\\?\\?\end{array}}\right]$$

Agar pada elemen baris ke-1 kolom ke-1 muncul angka satu terdapat 3 pilihan cara  :

1. Dengan menukarkan baris ke-1 dengan baris ke-3 \((R_{1}\leftrightarrow R_{3})\)
2. Dengan mengganti baris ke-1 dengan hasil kali baris ke-1 dengan \(\frac{1}{3}\) dinotasikan : \(\frac{1}{3}R_{1} \rightarrow R_{1}\)
3. Dengan mengganti baris ke-1 dengan hasil penjumlahan antara (hasil kali baris ke-2 dengan angka 1) dan (baris ke-1) dinotasikan : \((1)R_{2}+R_{1}\rightarrow R_{1}\)

Kita bebas memilih ketiga cara tersebut namun kita akan menggunakan cara ke-1. Sehingga jika kita kenakan operasi \((R_{1}\leftrightarrow R_{3})\), akan diperoleh :

Langkah 2

Sebagai acuan kita bisa membentuk matriks seperti ilustrasi berikut :

$$\left[{\begin{array}{ccc}1&?&?\\0&?&?\\?&?&?\end{array}}\right|\left.{\begin{array}{c}?\\?\\?\end{array}}\right]$$

Maka kita dapat menggunakan operasi \(2R_{1}+R_{2} \rightarrow R_{2}\). sehingga menjadi :

Langkah 3

Tujuan kita membentuk :

$$\left[{\begin{array}{ccc}1&?&?\\0&?&?\\0&?&?\end{array}}\right|\left.{\begin{array}{c}?\\?\\?\end{array}}\right]$$

Untuk membentuknya kita gunakan operasi \(-3R_{1}+R_{3}\rightarrow R_{3}\),

Langkah 4

Tujuan membentuk matriks :

$$\left[{\begin{array}{ccc}1&?&?\\0&1&?\\0&?&?\end{array}}\right|\left.{\begin{array}{c}?\\?\\?\end{array}}\right]$$

Dengan menggunakan operasi \(\frac{1}{8}R_{2} \rightarrow R_{2}\) maka didapat :

Langkah 5

Bentuk acuan :

$$\left[{\begin{array}{ccc}1&?&?\\0&1&?\\0&0&?\end{array}}\right|\left.{\begin{array}{c}?\\?\\?\end{array}}\right]$$

Dengan menggunakan operasi \(10R_{2} +R_{3} \rightarrow R_{3}\) sehingga kita peroleh :

Langkah 6

Bentuk acuan :

$$\left[{\begin{array}{ccc}1&?&?\\0&1&?\\0&0&1\end{array}}\right|\left.{\begin{array}{c}?\\?\\?\end{array}}\right]$$

Operasikan \(\frac{8}{46}R_{3} \rightarrow R_{3}\), maka kita dapatkan :

Langkah 7

Bentuk acuan :

\(\left[{\begin{array}{ccc}1&0&?\\0&1&?\\0&0&1\end{array}}\right|\left.{\begin{array}{c}?\\?\\?\end{array}}\right]\)

Kita gunakan operasi \(-3R_{2}+ R_{1}\rightarrow R_{1}\) untuk memperoleh :

Langkah 8

Bentuk acuan :

$$\left[{\begin{array}{ccc}1&0&?\\0&1&0\\0&0&1\end{array}}\right|\left.{\begin{array}{c}?\\?\\?\end{array}}\right]$$

Selanjutnya kita operasikan \(\frac{1}{8}R_{3}+R_{2}\rightarrow R_{2}\) untuk membentuk :

Langkah 9

Bentuk acuan :

$$\left[{\begin{array}{ccc}1&0&0\\0&1&0\\0&0&1\end{array}}\right|\left.{\begin{array}{c}?\\?\\?\end{array}}\right]$$

Langkah terakhir dengan mengoperasikan \(\frac{13}{8}R_{3} +R_{1} \rightarrow R_{1}\) dan kita peroleh :

Dari hasil diatas jelaslah didapat pemecahan :

Jadi pemecahan (solusi) dari sistem persamaan linear tersebut adalah \(x=1,y=2,z=3\) (solusi tunggal). Lalu bagaimana jika sistem tersebut mempunyai banyak solusi atau tidak mempunyai solusi?

Mari kita lihat contoh lain dimana pemecahannya tidak tunggal (banyak solusi).

Contoh 2 (Banyak Solusi)

Baca juga : Sistem Persamaan Linear Secara Umum

Didefinisikan sistem persamaan linear sebagai berikut :

\(6x_{1} -3x_{2}+2x_{3}=4\)
\(-5x_{1}+x_{2}+7x_{3}=5\)

Tentukan solusi dari sistem tersebut dengan menggunakan operasi baris elementer.

Penyelesaian :

Kita representasikan kedalam bentuk matriks, sehingga kita peroleh :

$$\left[{\begin{array}{ccc}6&-3&2\\-5&1&7\end{array}}\right|\left.{\begin{array}{c}4\\5\end{array}}\right]$$

Langkah 1

Bentuk acuan :

$$\left[{\begin{array}{ccc}1&?&?\\?&?&?\end{array}}\right|\left.{\begin{array}{c}?\\?\end{array}}\right]$$

Untuk merubahnya kita bisa menggunakan 2 cara :

1. Dengan mengganti baris ke-1 dengan hasil kali baris ke-1 dengan \(\frac{1}{6}\) atau dapat kita notasikan : \(\frac{1}{6}R_{1} \rightarrow R_{1}\)
2. Dengan mengganti baris ke-1 dengan hasil penjumlahan antara baris-1 dan ( hasil perkalian baris ke-2 dengan angka 1 ). Atau dapat dinotasikan : \((1)R_{2}+R_{1} \rightarrow R_{1}\)

Kita bebas memilih salah satu dari dua cara diatas, namun disini kita akan menggunakan cara ke-2 yaitu dengan operasi \((1)R_{2}+R_{1} \rightarrow R_{1}\), sehingga kita peroleh :

Langkah 2

Bentuk acuan :

$$\left[{\begin{array}{ccc}1&?&?\\0&?&?\end{array}}\right|\left.{\begin{array}{c}?\\?\end{array}}\right]$$

Kita kenakan operasi \(5R_{1} +R_{2} \rightarrow R_{2}\) untuk memperoleh :

Langkah 3

Bentuk acuan :

$$\left[{\begin{array}{ccc}1&?&?\\0&1&?\end{array}}\right|\left.{\begin{array}{c}?\\?\end{array}}\right]$$

Untuk mengubahnya kita bisa menggunakan operasi \(-\frac{1}{9}R_{2} \rightarrow R_{2}\) sehingga didapat :

Langkah 4

Bentuk acuan :

$$\left[{\begin{array}{ccc}1&0&?\\0&1&?\end{array}}\right|\left.{\begin{array}{c}?\\?\end{array}}\right]$$

Langkah terakhir dengan menggunakan operasi \(2R_{2} +R_{1}\rightarrow R_{1}\), untuk memperoleh :

Dari bentuk terkahir dapat juga ditulis:

Atau untuk sebarang bilangan \(x_{3}\) berlaku :

$$\begin{array}{c}x_{1}=-\frac{19}{9}+\frac{23}{9}x_{3}\\x_{2}=-\frac{50}{9}+\frac{52}{9}x_{3}\end{array}$$

Jadi himpunan penyelesaiannya yaitu :

Contoh 3 (Tidak Punya Solusi)

Diberikan sistem persamaan linear sebagai berikut :

\(1x+2y+1z=1\)
\(3x+6y+3z=2\)

Tentukan solusi dari sistem persamaan linear tersebut (bila ada).

Penyelesaian :

Pertama, kita representasikan kedalam bentuk matriks:

$$\left[{\begin{array}{ccc}\color{red}{1}&\color{red}{2}&\color{red}{1}\\\color{blue}{3}&\color{blue}{6}&\color{blue}{3}\end{array}}\right|\left.{\begin{array}{c}1\\2\end{array}}\right]$$

Langkah 1

Kita amati bahwa koefisien-koefisien dari baris ke-2 (biru) merupakan kelipatan dari koefisien-koefisien pada baris ke-1 (merah).

Sehingga kita bisa gunakan operasi \(-3R_{1}+R_{2}\rightarrow R_{2}\) dan kita peroleh :

Dari bentuk terakhir diatas diperoleh sistem persamaan linear baru yaitu

Perhatikan pada persamaan kedua, berapapun nilai dari \(x,y\) dan \(z\), maka nilai dari

$$(0)x + (0)y +(0)z = 0$$

Karena \( 0 \neq -1\) akibatnya persamaan kedua tidak punya solusi. Kemudian karena persamaan kedua merupakan bagian dari sistem baru tersebut akibatnya sistem baru tersebut juga tidak punya solusi.

Mengingat kembali dengan Operasi Baris Elementer sistem awal dan sistem baru yang terbentuk mempunyai solusi yang sama. Jadi jika sistem baru tersebut tidak mempunyai solusi maka sistem persamaan linear pada contoh ke-3 (awal) juga tidak punya solusi.

Disarankan membaca : Pengenalan Operasi Baris Elementer

Kesimpulan

Pada dasarnya pemecahan Sistem Persamaan Linear (SPL) dengan metode Operasi Baris Elementer (OBE) memiliki tujuan membentuk sistem persamaan linear baru yang mempunyai solusi yang sama dengan pemecahan yang lebih mudah. Kita akan terbiasa dengan metode ini jika kita mau mencobanya berkali-kali.

Catatan : Terkadang saat melakukan operasi baris elementer kita akan berhadapan dengan bentuk pecahan. Sehingga disarankan untuk menghitungnya dengan teliti, karena akan mempengaruhi langkah-langkah selanjutnya.